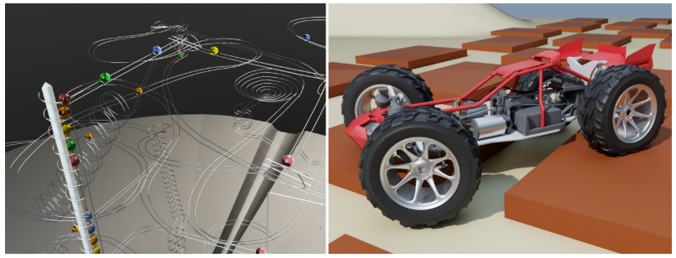
📄 论文：Detailed Rigid Body Simulation with Extended Position Based Dynamics

引言

刚体物理仿真是游戏引擎以及CG特效中一个极为重要的功能。然而为了实现刚体运动的模拟，我们通常需要求解一些极为复杂的数学公式：

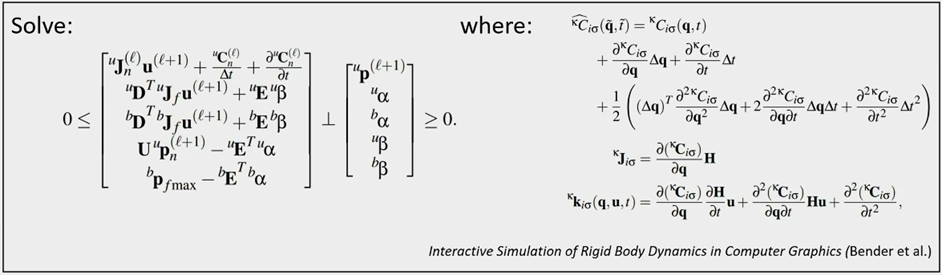
难道只有数学巫师才配研究刚体物理仿真吗？😿

基于位置的动力学（Position Based Dynamics, PBD）^[2]是Müller等人于2006年发表的一种物理仿真方法。此前的方法都是基于力进行解算的，而PBD方法的独特点则在于它选择基于位置进行解算。

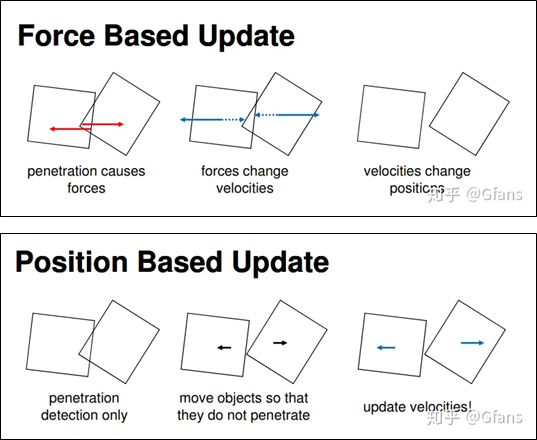
这样做有很多好处，一个是避免加速度到速度，速度到位置的多次积分，因而提升性能；另一方面则是具有更好的可控性，比如下图中，为了将两个碰撞的物体分离，基于力的方法需要很精妙的设计，才能找到一个合适的力将两个物体分离开。而基于位置的方法，直接将物体挪走就完成了。除此之外，PBD方法还具有易于实现、稳定的优点，这使其十分契合实时应用的需求。

PBD方法是基于粒子的。仿真场景中的所有物体都由粒子组成，再加上各类约束（Constraint），保证物体满足特定的性质。因此，PBD方法可以在一套统一的框架下同时模拟刚体、布料、软体、流体等不同物理性质的物体极及其交互^[3]。

PBD使用粒子表示各种物体，这使得其实现相比传统物理引擎会简单很多。因为所有的计算操作，都只需要针对没有旋转自由度的球体进行。然而，这也是PBD方法的一个缺点。使用粒子表示物体，意味着物体的体积越大，需要的粒子越多，这使其Scalability较差。并且，基于粒子的方法难以实现稳定的冲量传导和关节效果。

本论文名为Detailed Rigid Body Simulation with Extended Position Based Dynamics^[1]，目标就是在继承PBD方法的简单性的同时，加入对任意形状刚体以及关节效果的支持。

思考

刚体和粒子的区别其实不大。粒子因为是完全对称的，所以不需要考虑角度和角速度。而刚体则因为可能具有任意的形状，在受力时需要加入对角度和角速度的计算。

传统物理引擎的复杂性，主要是因为使用了Global Solver，也就是企图使用一个矩阵连立所有已知方程，一下子把所有物体的物理更新计算出来。求解矩阵对于计算机来说很简单，但是对于人类的理解而言则带来了很多困难。所以本文想要继续采取PBD方法的Local Solver，以每个物体为单位，单独的进行迭代求解。

关于Global Solver和Local Solver的区别可见下图。左边是Global Solver，在一次迭代中会考虑所有的Constraint一并进行更新，即$\nabla C_1+\nabla C_2$。右边是Local Solver，每次迭代会依次遍历所有Constraint，分别进行更新，也就是交替的修正$\nabla C_1$和$\nabla C_2$。

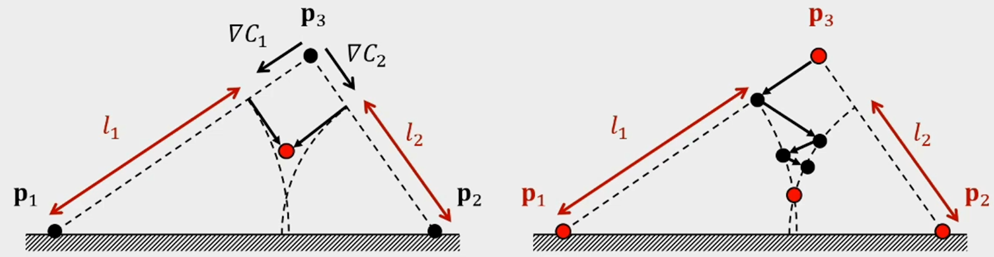
Local Solver可能存在一会南辕，一会北辙的情况，所以以往Local Solver的缺陷在于收敛速度相对较慢。而PBD方法就在前几年引入了sub-stepping^[4]的机制，可以在很大程度上缓解收敛速度慢的问题。

改进

这篇文章的主要增量工作，就是在原来只考虑位置和速度更新的PBD方法中，加入了角度和角速度的更新。下图左侧是PBD方法中的步骤，右边是本文的增量工作。可以看出角速度和速度其实是很类似的，只是需要涉及到转动惯量等角度专用的物理属性。

同理，约束相关的公式也需要加入对角度相关属性的计算，就可以实现支持通用刚体形状的各类约束，把这些约束像API一样使用，就可以实现包括Attachment, Contact, Static Friction, Hinge Joint等效果。

本文中的方法在Core-i7 CPU @ 3.6GHz的CPU上就可以达到实时的性能。

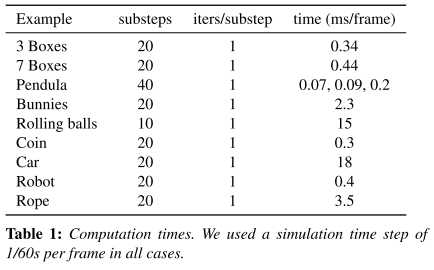
并且因为PBD本身是一种类似于隐式的方法，所以可以很好的保留空间及时间维度上的细节。比如下图中，本文的方法可以稳定模拟一堆玻璃珠在高度复杂的轨道形状上滚动的效果。而传统的方法要么性能太差，要么会遭受穿透。

总结

本文提出了一种基于PBD的通用物理引擎框架，相比传统物理引擎更加容易实现，并且能更好的保留时空细节。继承了XPBD方法的简单性和能够处理无限刚硬（Infinitely stiff）关节的优点。通过substepping，能够在一个时间步内处理大质量比的物体交互以及快速的转动变化。

目前的缺陷在于substepping会使得一些过高频率的扰动也被保留下来，在特定情况下会让人看到物体在颤动。另外一方面是在模拟大量层层相叠的物体时会有不稳定的情况，这也是本文的未来研究方向。

引用

1. Müller, Matthias, et al. "Detailed rigid body simulation with extended position based dynamics." Computer Graphics Forum. Vol. 39. No. 8. 2020.
2. Müller, Matthias, et al. "Position based dynamics." Journal of Visual Communication and Image Representation 18.2 (2007): 109-118.
3. Macklin, Miles, et al. "Unified particle physics for real-time applications." ACM Transactions on Graphics (TOG) 33.4 (2014): 1-12.
4. Macklin, Miles, et al. "Small steps in physics simulation." Proceedings of the 18th annual ACM SIGGRAPH/Eurographics Symposium on Computer Animation. 2019.