PageRank: The algorithm behind Google search engine

📄 You can download PDF version for better readability

Contents

1 Introduction

The World Wide Web is a great invention that benefits all of us today. Anyone can share information online with nearly zero cost. However, the convenience of publishing websites also leads to trouble. Since web pages proliferate free of quality control or publishing cost, the Internet is flooded with useless or even harmful information.

Luckily, search engines come to our rescue. Just by typing in the keyword, the search engine will find the most relevant pages for us automatically and instantly. Highest mountain, tallest man on earth, favorite food of a celebrity. Google is capable of answering a large variety of questions.

But have you ever considered how do the search engines work? How is it possible that search engines can figure out what web pages are most likely useful to you among billions of web pages? Suppose you are searching for “SJTU” on Google, what logic and algorithm make Google decide to put the home page of SJTU on top of everything else?

PageRank^[1] is one of the algorithm that is responsible for these decisions. It is developed by Larry Page and Sergey Brin (founders of Google) at Stanford University in 1996 and became one of the most famous and fundamental algorithms behind the Google search engine.

In a nutshell, PageRank is a link analysis algorithm that assigns numerical weights to each element of a hyperlinked set of documents, with the purpose of measuring its relative importance within the set ^[2].

In the following sections, we will describe PageRank in more detail.

2 PageRank

2.1 Definition

The basic idea of PageRank is that the importance of a web page depends on the pages that link to it.

Given page $A$, if there are a lot of pages link to this page, then it is considered important on the web. On the other hand, if page $A$ has only one backlink, but this link is from an authoritative web page $B$ (such as www.bbc.com or www.yahoo.com), we also think $A$ is important because page $B$ can transfer its popularity or authority to $A$.

In the PageRank algorithm, the connections between web pages are represented by a graph. Each web page is considered as a vertex, and each hyperlink is considered as a directed edge. Forward links correspond to out-edges, and backlinks correspond to in-edges. Links from a page to itself are ignored. Multiple outbound links from one page to another page are treated as a single link.

With these intuitions, we begin by defining a simple ranking $SPR$, which is a slightly simplified version of PageRank.

Definition 1 (Simple PageRank). Let $u$ be a web page. $F_u$ is the set of pages $u$ points to, and $B_u$ is the set of pages that points to $u$. Let $N_u = |F_u|$ be the number of links from $u$. Then, the Simple PageRank of a set of Web pages is an assignment SPR to the Web pages which satisfies

\begin{equation} \begin {split} SPR(u) &= \sum_{v \in B_u} \frac{SPR(v)}{N_v} \\ \sum_{u\in V}SPR(u) &= 1 \end {split} \end{equation}

Note that the rank of a page is divided among its forward links evenly to contribute to the ranks of the pages they point to.

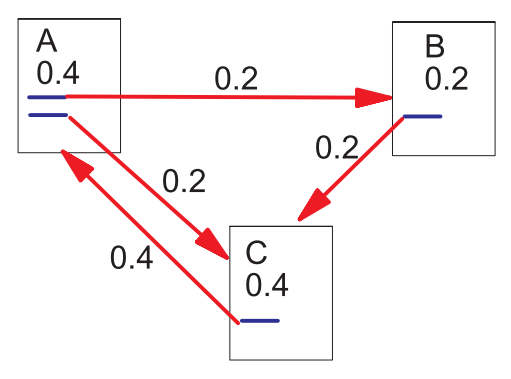
Now let’s look at an example to see how this works. Suppose there are three web pages $A$, $B$, and $C$. $A$ has two edges to $B$ and $C$. $B$ has one edge to $C$, and $C$ has one edge to $A$.

Since $A$ has two out-edges, it contributes half of its rank to $B$ and $C$. $B$ and $C$ on the other hand, have only one out-edge, thus they give all of their ranks to the target. Therefore, we can easily calculate the PageRank for each page.

\begin{equation} \begin{split} SPR(A) &= SPR(C) = 0.4\\ SPR(B) &= \frac{SPR(A)}{2} = 0.2 \\ SPR(C) &= \frac{SPR(A)}{2} + SPR(B) = 0.4 \\ \end{split} \end{equation}

Figure 1 demonstrate the graph representation for this example.

However, there are some problems with this simplified ranking function ^[3].

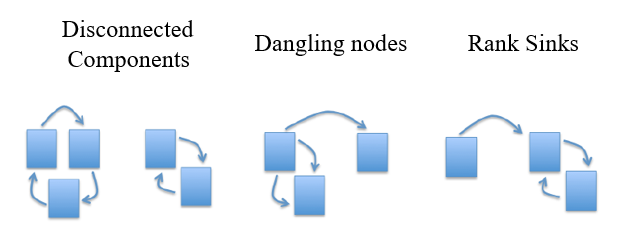
Disconnected Components. If our web graph has two or more disconnected components, the rank from one component has no way to get into the other component. This means the initial assignment of rank will influence the final ranking assignment in the stable state.

Dangling Nodes. There are some pages that do not have any out-links (referred to as dangling nodes), and the importance received by these pages cannot be propagated. They affect the model because it is not clear where their weight should be distributed, and there are a large number of them. Often these dangling nodes are simply pages that have not been downloaded yet since it is hard to sample the entire web.

Rank Sinks. Consider two web pages that point to each other but to no other page. And suppose there are some web pages which point to one of them. Then, during iteration, the loop will accumulate rank but never distribute any rank (since there are no out-edges). The loop forms a sort of trap that we call a rank sink.

To solve the dangling nodes problem, dangling nodes are assumed to link out to all other pages in the collection. Their PageRank scores are therefore divided evenly among all other pages. In other words, to be fair with pages that are not dangling, these random transitions are added to all nodes in the Web.

In order to deal with the problem with rank sinks and disconnected components, a positive constant $d$ between 0 and 1 (typically set to 0.85 ^[4]) is introduced, which we call the damping factor.

Finally, the definition of PageRank is modified as follows:

Definition 2 (PageRank). Let $u$ be a web page. $F_u$ is the set of pages $u$ points to, and $B_u$ is the set of pages that points to $u$. Let $N_u = |F_u|$ be the number of links from $u$. Then, the PageRank of a set of Web pages is an assignment PR to the Web pages which satisfies

\begin{equation} \begin{split} PR(u) &= \frac{1-d}{N} + d\big(\sum_{v \in B_u} \frac{PR(v)}{N_v}\big) \\ \sum_{u\in V}PR(u) &= 1 \end{split} \end{equation}

2.2 Matrix Forms

Let $A$ be a square matrix with the rows and columns corresponding to web pages. We define the entries of matrix $A$ by

\begin{equation} A_{u,v} = \left\{ \begin{array}{rcl} \frac{1}{N_u} & & {\text{if there is an edge from v to u,}}\\ \frac{1}{N-1} & & {\text{if node v is a dangling node and } u \ne v}\\ 0 & & {\text{otherwise,}} \end{array} \right. \end{equation}

We treat $R$ as a vector over web pages, that is

\begin{equation} R = \left[ \begin{matrix} PR(u_1) \\ PR(u_2) \\ \vdots \\ PR(u_n) \end{matrix} \right] \end{equation}

Finally, we have the following matrix equation to calculate PageRank for all web pages.

\begin{equation} R = \frac{1-d}{N} \mathbf{1}+ dAR \end{equation}

where $\mathbf 1$ is the vector consisting of all ones.

2.3 Random Surfer Model

The definition of PageRank above has another intuitive basis in random walks on graphs. The random surfer simply keeps clicking on successive links at random. The simplified version corresponds to the standing probability distribution of a random walk on the graph of the Web.

However, if a real Web surfer ever gets into a small loop of web pages, it is unlikely that the surfer will continue in the loop forever. Instead, the surfer will jump to some other page. The additional parameter $d$ can be viewed as a way of modeling this behavior: the surfer periodically “gets bored” and jumps to a random page.

2.4 Calculation Method

PageRank can be computed either iteratively or algebraically ^[2]. The iterative method can be viewed as the power iteration or the power method. The basic mathematical operations performed by these two methods are similar.

2.4.1 Power Method

At $t=0$, an initial probability distribution is assumed, usually

\begin{equation} PR(u_i;0) = \frac{1}{N} \end{equation}

where $N$ is the total number of pages, and $PR(u_i;0)$ denotes rank for page $u_i$ at time 0.

At each time step, the computation, as detailed above, yields

\begin{equation} PR(u_i;t+1) = \frac{1-d}{N} + d\left(\sum_{v \in B_{u_i}} \frac{PR(v;t)}{N_v}\right) \end{equation}

or in matrix notation

\begin{equation} R(t+1) = \frac{1-d}{N} + dAR(t) \label{eq:matrix} \end{equation}

Since $R$ is a probability distribution (i.e.$|R|=1$), we have

\begin{equation} \begin{split} ER &= \mathbf 1 \times (PR(u_1) + PR(u_2) + ... + PR(u_n)) \\ &= \mathbf 1 \end{split} \end{equation}

where $\mathbf 1$ is a vector of all ones, and $E$ is a matrix of all ones.

Therefore, Equation 9 can be rewrite as

\begin{equation} R(t+1) = (\frac{1-d}{N}E + dA)R(t) \label{eq:complex_matrix} \end{equation}

Let $`$\hat A = \frac{1-d}{N}E + dA$`$, and Equation 11 can be further simplified as

\begin{equation} R(t+1) = \hat A R(t) \end{equation}

Now we can see that the PageRank $R$ we want to calculate is actually the principal eigenvector of matrix $\hat A$ with eigenvalue $1$.

The probability calculation is repeated for several iterations until convergence is achieved, that is

\begin{equation} |R(t+1)-R(t)|<\epsilon \end{equation}

2.4.2 Algebraic Method

For $t\rightarrow\infty$ (i.e., in the steady state), Equation 9 can be rewrite as

\begin{equation} R = \frac{1-d}{N} \mathbf 1 + dAR \end{equation}

Hence,

\begin{align} (I-dA) R &= \frac{1-d}{N} \mathbf 1 \\ R &= (I-dA)^{-1} \frac{1-d}{N} \mathbf 1 \end{align}

where $I$ is the identity matrix.

The solution exists and is unique for $0 < d < 1$. This can be seen by noting that $A$ is by construction a stochastic matrix (i.e. the elements of each column sum up to 1) and hence has an eigenvalue equal to one as a consequence of the Perron-Frobenius theorem.

However, since the time complexity of matrix inversion is $O(n^3)$, this method is impractical for industrial usage where billions of webpages are involved.

3 Key Properties

3.1 Proof of Convergence

Claim 3. The power method for calculating PageRank always converge to true solution for any given $\epsilon$ (error tolerance parameter) ^[5].

Proof. First, we define $`$R^\star$`$ as the true PageRank assignments, and $PR^\star(v)$ as the true PageRank for page $v$. We have

\begin{equation} R^\star = \left[ \begin{matrix} PR^\star(u_1) \\ PR^\star(u_2) \\ \vdots \\ PR^\star(u_n) \end{matrix} \right] \end{equation}

Then we can define the total error at step $t$ to be:

\begin{equation} Err(t) = \sum_{v \in V} |PR(v;t)-PR^\star(v)| \end{equation}

Since $PR^\star$ is the true solution, we know that it must satisfy the PageRank equations exactly:

\begin{equation} PR^\star (u) = \frac{1-d}{N} + d\left(\sum_{v \in B_u}\frac{PR^\star (u)}{N_v}\right) \end{equation}

To find the error between true solution and current time step, we subtract this from the iterative method equation, and obtain:

\begin{equation} PR(u;t) - PR^\star (u) = d\left(\sum_{v \in B_u}\frac{PR(u;t-1) - PR^\star (u)}{N_v}\right) \end{equation}

Using the Triangle Inequality, we can get this expression for the error in PageRank $v$ at step $t$:

\begin{equation} |PR(u;t) - PR^\star (u)| \le d\left(\sum_{v \in B_u}\frac{|PR(u;t-1) - PR^\star (u)|}{N_v}\right) \end{equation}

Now we can sum over all v to get the total error $Err(t)$. Notice that the page $v$ will occur $N_v$ times on the right-hand side, and since there is also a $N_v$ on the denominator, they will cancel each other.

\begin{equation} \begin{split} Err(t) &= \sum_{u \in V} |PR(u;t) - PR^\star (u)| \\ &\le d \left( \sum_{v\in B_u} |PR(u;t-1) - PR^\star (u)| \right) \end{split} \end{equation}

We are left with $d$ times the total error at time $t-1$ on the right-hand side.

\begin{equation} Err(t) \le d Error(t-1) \end{equation}

This shows fast convergence of power method, because the decrease in total error is compounding. From this inequality, we can also see that the damping parameter $d$ is essential for convergence.

3.2 Time Complexity

PageRank is computed for several iterations until termination condition $Err(t) \le \epsilon$ is met. In each iteration, every vertex will compute a new PageRank by accumulating all of its neighbors’ contributions. Thus the time complexity of one iteration is $O(m+n)$, where $n$ is the number of vertices, and $m$ is the number of edges.

In the following, we prove that there exists an upper bound for the number of iterations.

Claim 4. The number of iteration is bounded by $`$log_d(\frac{\epsilon}{n})$`$, where $n$ is the number of vertices, $\epsilon$ is the tolerance parameter, and $d$ is the damping factor.

Proof. According to our previous analysis on convergence, we have

\begin{align} Err(t) &= \sum_{v \in V} |PR(v;t)-PR^\star(v)| \label{eq:err} \\ Err(t) &\le d Error(t-1) \label{eq:reduction} \end{align}

Since $PR(v;t)\in [0,1]$, From equation 24 we can obtain

\begin{equation} Err(0) = \sum_{v \in V} |PR(v;0)-PR^\star(v)| \le \sum_{v \in V} 1 \le n \end{equation}

Combinated with Equation 25, and we get

\begin{equation} Err(t) \le d Error(t-1) \le d^t Error(0) \le d^t n \label{eq:dtn} \end{equation}

The condition for iteration to terminate is

\begin{equation} Err(t) \le \epsilon \label{eq:eps} \end{equation}

Putting Equation 27 and 28 together and we obtain an upper bound for iteration number $t$.

\begin{align} d^tn &\le \epsilon \\ t &\le log_d(\frac{\epsilon}{n}) \end{align}

Finally, since the number of iteration is bounded by $`$log_d(\frac{\epsilon}{n})$`$, and the time complexity of one iteration is $O(m+n)$, the total time complexity of PageRank is $`$O((m+n)log_d(\frac{\epsilon}{n}))$`$.

According to the original paper ^[1], PageRank on a large 322 million link database converges to a reasonable tolerance in roughly 52 iterations. The convergence on half the data takes roughly 45 iterations. This suggests that PageRank will scale very well even for an extremely large collection.

The actual time complexity for industrial use can get quite more complex. Due to the large scale of webpages, the graph can hardly be stored in memory on a single machine. Distributed algorithms such as ^[6] are developed to solve this problem.

4 Conclusion

4.1 Summary

In this note, we described PageRank, a ranking algorithm for webpages based on their importance. The intuition behind PageRank is that it uses information that is external to the Web pages themselves - their backlinks, which provide a kind of peer review ^[1]. PageRank works by counting the number and quality of links to a page to determine a rough estimate of how important the website is. The underlying assumption is that more important websites are likely to receive more links from other websites.

First, we show a simplified version of PageRank, which works well in some cases, but can’t handle problems like dangling nodes, rank sinks, and disconnected components. Therefore, the damping factor and some other modifications are introduced to solve these problems.

The behavior of PageRank can be thought of as modeling the behavior of a random surfer. The random surfer simply keeps clicking on successive links at random, and the PageRank corresponds to the standing probability distribution.

PageRank can be calculated iteratively or algebraically. However, the algebraical method is time-consuming since it involves matrix inversion, making it impractical for industrial usage. Iterative methods such as Power Method are preferred, and gives an approximate result for PageRank with much better performance. The proof of convergence and time complexity analysis for the iterative method is described in detail in Section 3.

PageRank method was developed to evaluate the importance of web-pages via their link structure. The mathematics of PageRank, however, is entirely general and applies to any graph or network in any domain ^[7]. Thus, PageRank is now regularly used in other fields, such as bibliometrics, social and information network analysis, link prediction, and recommendation.

4.2 Extensions

Following the discovery of PageRank, there has been a huge amount of work to improve or extend PageRank. Here are a few:

• Intelligent Surfing^[8]. This paper proposes a method to improve PageRank by using a more intelligent surfer, one that is guided by a probabilistic model of the relevance of a page to a query.
• TrustRank^[9]. Web spam pages use various techniques to achieve higher-than-deserved rankings in a search engine’s results. This paper proposes techniques to semi-automatically separate reputable, good pages from spam.
• PigeonRank^[10]. PigeonRank is developed by Google to provide preference to local search results. This is quite useful for the user and local businesses.
• Fast Distributed PageRank Computation^[6]. Due to the large scale of webpages, PageRank can benefit a lot from distributed computation. This paper presents fast random walk-based distributed algorithms for computing PageRanks in general graphs and prove strong bounds on the round complexity.

References

1. Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd. The pagerank citation ranking: Bringing order to the web. Technical report, Stanford InfoLab, 1999.
2. Wikipedia contributors. Pagerank — Wikipedia, the free encyclopedia. https://en.wikipedia.org/w/index.php?title=PageRank&oldid=961815901, 2020. [Online; accessed 14-June-2020].
3. Ryan Tibshirani. Pagerank. https://www.stat.cmu.edu/~ryantibs/datamining/lectures/03-pr.pdf, 2013.
4. Sergey Brin and Lawrence Page. The anatomy of a large-scale hypertextual web search engine. 1998.
5. Rio Goodman. Lecture 10: Pagerank. https://web.stanford.edu/~ashishg/msande235/spr08_09/Lecture10.pdf, 2009.
6. Atish Das Sarma, Anisur Rahaman Molla, Gopal Pandurangan, and Eli Upfal. Fast distributed pagerank computation. In International Conference on Distributed Computing and Networking, pages 11–26. Springer, 2013.
7. David F Gleich. Pagerank beyond the web. SIAM Review, 57(3):321–363, 2015.
8. Matthew Richardson and Pedro Domingos. The intelligent surfer: Probabilistic combination of link and content information in pagerank. In Advances in neural information processing systems, pages 1441–1448, 2002.
9. Zoltan Gyongyi, Hector Garcia-Molina, and Jan Pedersen. Combating web spam with trustrank. In Proceedings of the 30th international conference on very large data bases (VLDB), 2004.
10. Wikipedia contributors. Google pigeon — Wikipedia, the free encyclopedia. https://en.wikipedia.org/w/index.php?title=Google_Pigeon&oldid=945252161, 2020. [Online; accessed
    15-June-2020].